参考文献:
1. 堆的概念
如果有一个关键码的集合 K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质
-
堆中某个节点的值总是不大于或不小于其父节点的值;
-
堆总是一棵完全二叉树。

2. 存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储,
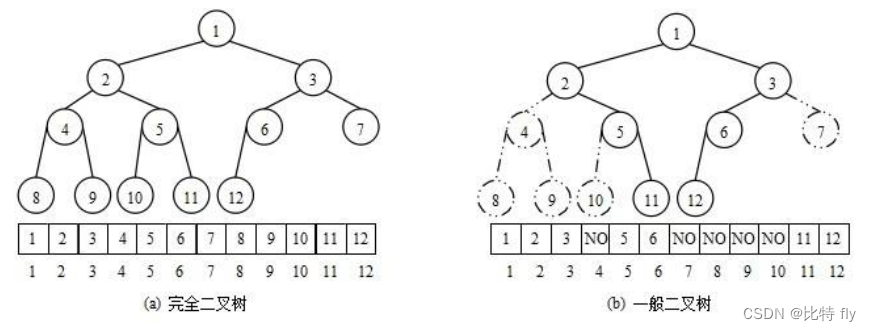
对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树章节的性质对树进行还原。假设 i 为节点在数组中的下标,则有:
- 如果 i 为0,则i表示的节点为根节点,否则i节点的双亲节点为
(i - 1)/2 - 如果
2 * i + 1小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子 - 如果
2 * i + 2小于节点个数,则节点 i 的右孩子下标为2 * i + 2,否则没有右孩子
3. 堆的创建
3.1 堆的向下调整
对于集合 { 27,15,19,18,28,34,65,49,25,37 } 中的数据,如果将其创建成堆呢?
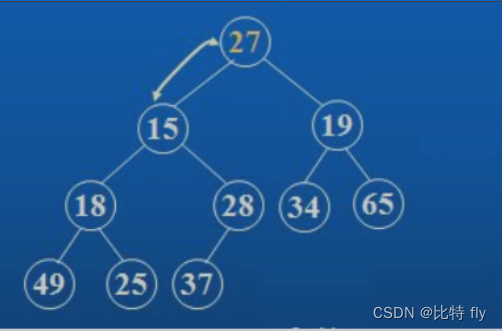
仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。
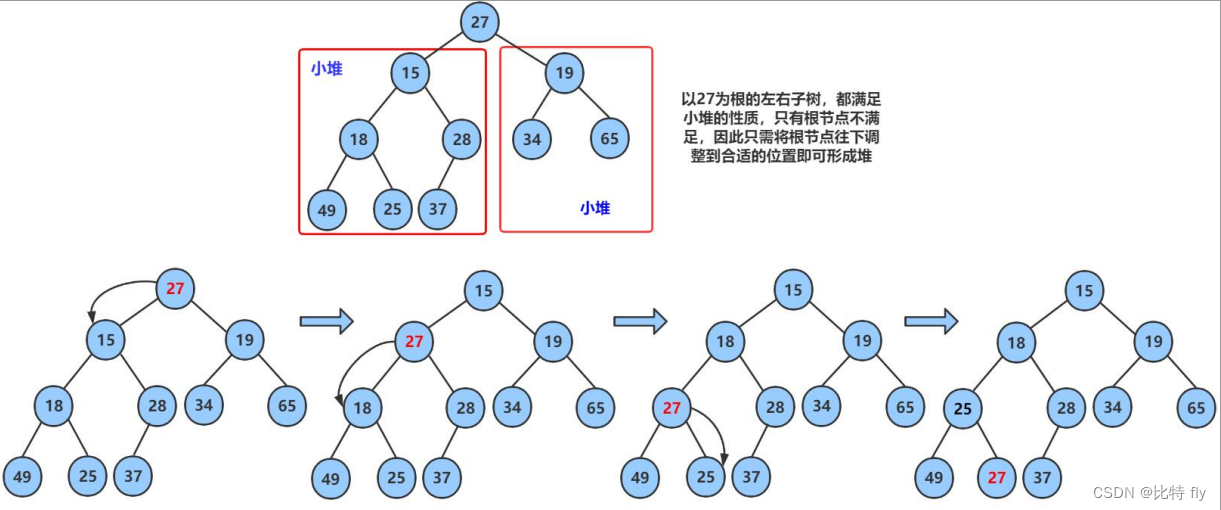
向下过程(以小堆为例):
- 让 parent 标记需要调整的节点,child 标记 parent 的左孩子(注意:parent 如果有孩子一定先是有左孩子)
- 如果 parent 的左孩子存在,即:
child < size, 进行以下操作,直到 parent 的左孩子不存在- parent 右孩子是否存在,存在找到左右孩子中最小的孩子,让 child 进行标
- 将 parent 与较小的孩子 child 比较,如果:
- parent 小于较小的孩子 child,调整结束
- 否则:交换 parent 与较小的孩子 child,交换完成之后,parent 中大的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即
parent = child;child = parent*2+1;然后继续2。
3.2 堆的创建
3.2.1 自顶向下建堆
这种建堆的方法具有 O(nlogn) 的时间复杂度。从根结点开始,然后一个一个的把结点插入堆中。当把一个新的结点插入堆中时,需要对结点进行调整,以保证插入结点后的堆依然是大根堆。
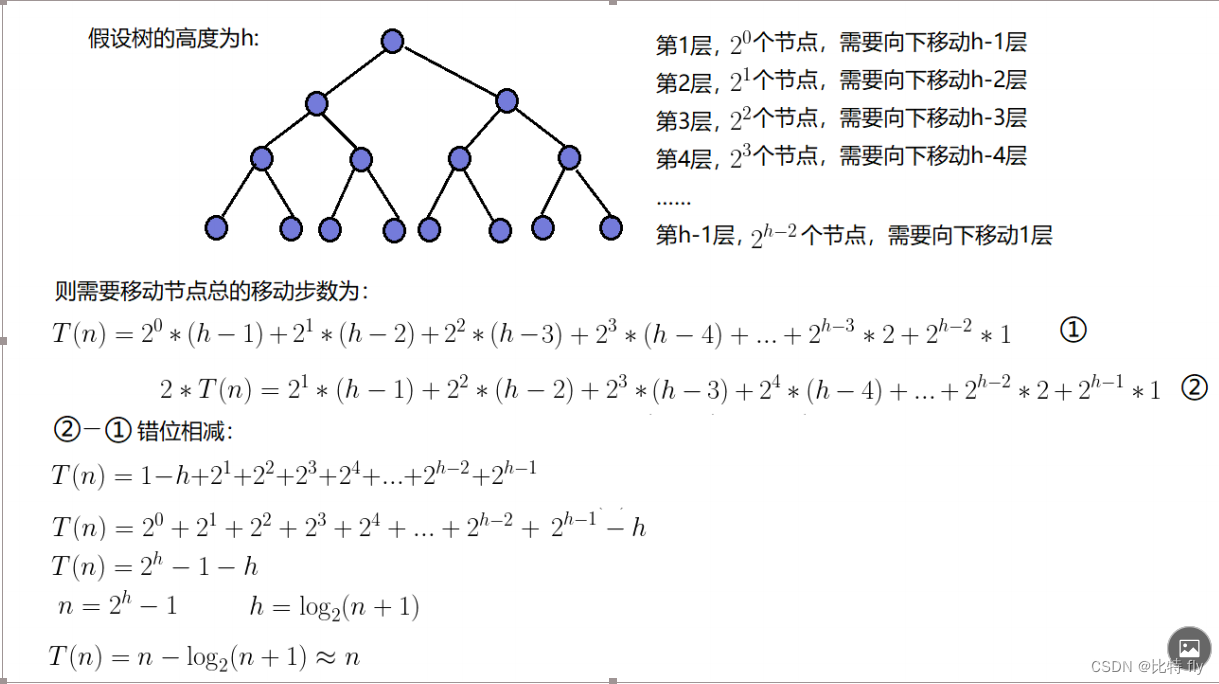
其中 h = log2(n+1)-1,第 k 层结点个数为 2k 个(当然最后一层结点个数可能小于 2h)。第 k 层的一个结点插入之后需要进行的比较(移动)次数为 k。于是总的比较(移动)次数为 ∑k*2k(k = 0,1,2,…,h)。可以求得 ∑k*2k(k = 0,1,2,…,h)=(log2(n+1)-2)*(n+1)+2 = O(n*log2n)
3.2.2 自下向上建堆
这种建堆的方法具有 O(n) 的时间复杂度。从第一个非叶子结点开始进行判断该子树是否满足堆的性质。如果满足就继续判断下一个点。否则,如果子树里面某个子结点有最大元素,则交换他们,并依次递归判断其子树是否仍满足堆性质。
4. 堆的插入与删除
4.1 堆的插入
堆的插入总共需要两个步骤:
- 将元素插入队尾
- 向上调整
我们通过一个插入例子来看看插入操作的细节。我们将数字16插入到这个堆中:

第一步是将新的元素插入到堆的队尾。则堆变成:

不幸运的是,现在堆不满足堆的属性,因为 2 在 16 的上面,我们需要将大的数字在上面(这是一个最大堆),为了恢复堆属性,我们需要交换16和2。
现在还没有完成,因为 10 也比 16 小。我们继续交换我们的插入元素和它的父节点,直到它的父节点比它大或者我们到达树的顶部,最后我们得到的堆:
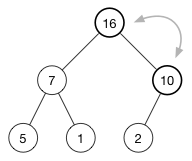
4.2 堆的删除
注意:堆的删除一定删除的是堆顶元素。具体如下:
- 将堆顶元素对堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
我们将这个树中的 (10) 删除:
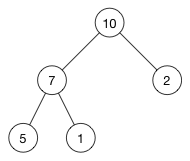
现在顶部有一个空的节点,怎么处理?

当插入节点的时候,我们将新的值返给数组的尾部。现在我们来做相反的事情:我们取出数组中的最后一个元素,将它放到树的顶部,然后再修复堆属性。
现在被删除位置处的元素值为1,由于它没有父节点,所以我们只把它与子节点进行比较,看是否违反了最大堆的属性:现在有两个数字( 7 和 2)可用于交换。我们选择这两者中的较大者称为最大值放在树的顶部,所以交换 7 和 1,现在树变成了:

继续堆化直到该节点没有任何子节点或者它比两个子节点都要大为止。对于我们的堆,我们只需要再有一次交换就恢复了堆属性:

